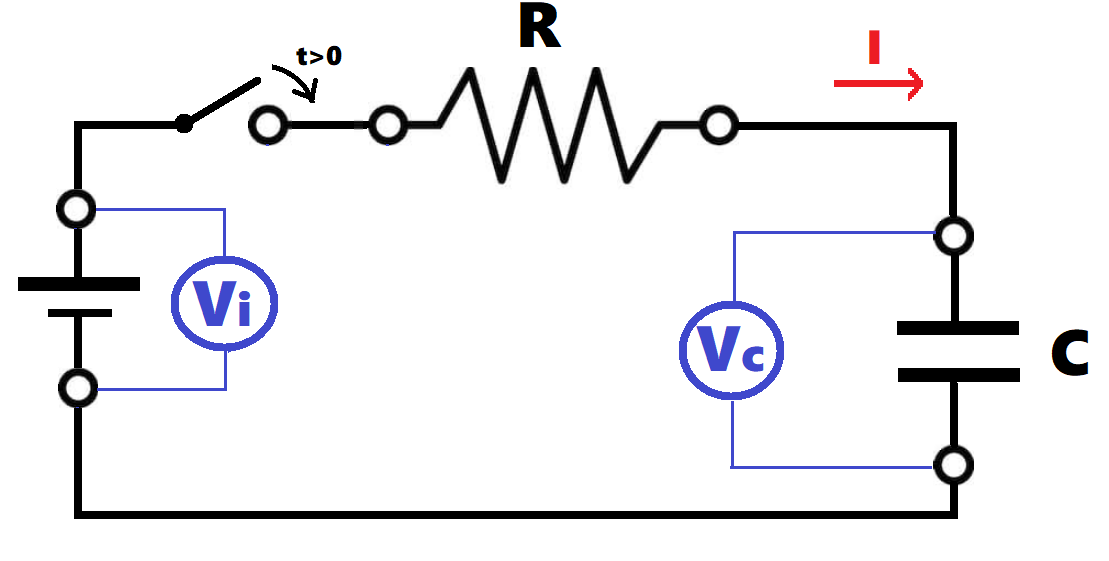
RC charging circuit

Calculator

Enter the value for the power supply voltage (Vi), resistor (R), and capacity (C). The value for the time constant (RC) and the capacitor energy will be calculated.
Optionally, the elapsed time from the moment the switch was closed can be entered. Voltage and current corresponding to that instant will be shown on the graph.

Initial data:
Vi: V
R:
C:
English

Resultados:
Time
constant (RC):		 s
Energy: J
Máx.current: A

Time: seconds


Theory

First we close the switch on the above circuit. At that moment, the capacitor, which had zero charge, start receiving electric charges and current is maximum, we could consider that the capacitor is behaving as a perfect conductor (initial current is Ii= Vi/R, equivalent to a circuit without the capacitor). However, this situation cannot be maintained, as soon as the capacitor stars increasing its charge, the current progressively diminishes, and after an infinite period of time the current will be zero.
The behaviour of the voltage is the opposite, initially the voltage between the capacitor terminals is zero, as we can consider that the capacitor is a perfect conductor. After an infinite period of time the current will be zero, so there will not be any voltage drop in the resistor and the capacitor voltage will be the same as the power supply.

Equations: The instant values for the current and voltage are:
    I = Vi/R x e(-t/RC)
    V = Vi x ( 1-e(-t/RC) )
Time Constant (RC): The time needed by the capacitor to be charged is proportional to R and C. The time constant (designated by τ or RC) is defined as the product of the resistor by the capacity.
    τ = R x C
Time constant is only a very useful reference to compare the time required by a capacitor to be charged. We usually consider that 5x RC (5τ) is enough time to a complete charge of a capacitor (more than 99%)

Links: