Resistor to be connected to LEDs
Introduction
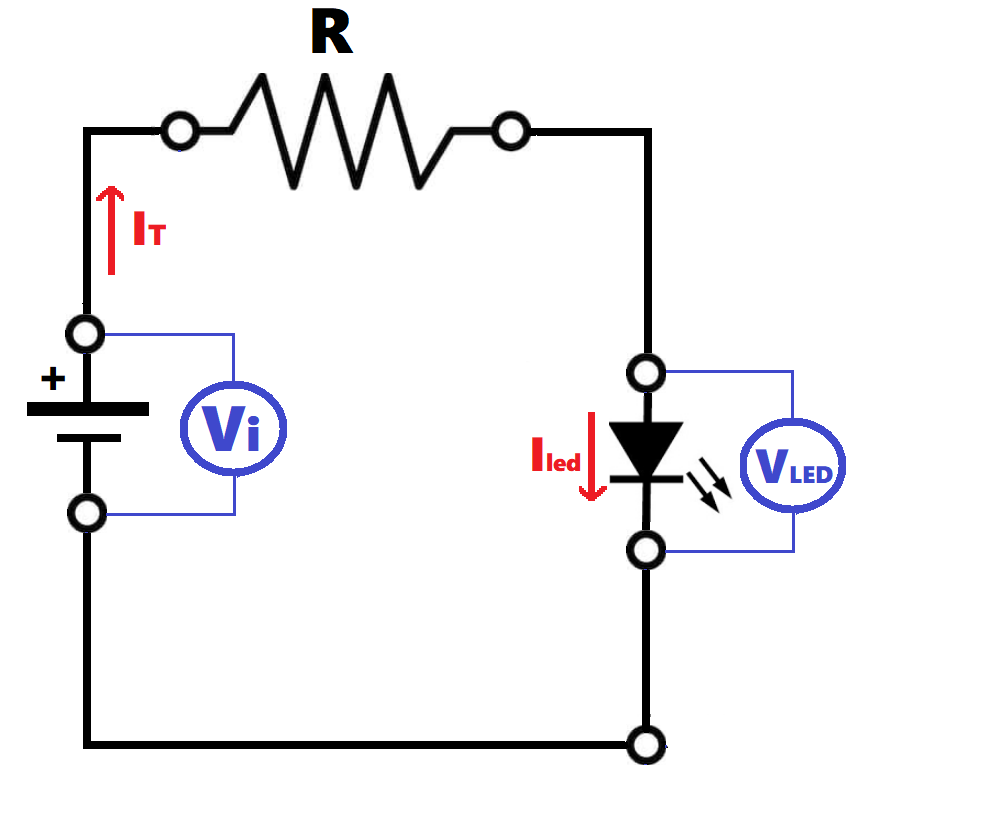
We always need to connect a resistor in series with our LEDs to protect and to limit the corrent through them. If several LEDs are connected in series or in parallel, a single resistor can be used for all of them:Calculator
Explanation
For this calculation, we use the Ohm's law (V = R-I). First, we need to know the voltage and current required for the LED diode. This information comes from the LED data sheet. Then we have to calculate the current that must flow through the resistor. If there is only one LED the current through the resistor (IT) equals the current through the LED (Iled) and the supply voltage (Vi) is the same than the voltage drop on the resistor plus the voltage drop on the LED:- Vi= Vled + VR
The value of the resistance is obtained simply by applying Ohm's law:
- R = VR/IT
Now we need to find out the voltage of the resistor. To do this, bear in mind that, unlike the currents, the voltages of elements in series add up.
The total power is calculated using the following equation PT= ViĀ· IT
The resistor power can be calculated with PR= R Ā· IT2. This value is important as we have to use a resistor that is able to dissipate at least this power.
Note that if we have a supply voltage big enough, the total power consumption (PT) of a set of LEDs in series probably can be much lower that when they are connected in parallel. However, it is only possible to connect LEDs in series when Vi > Vled Ā· N. In other case we would not have enough voltage to poser the LEDs.
Typically, the voltage drop for a LED is between 1.8 and 3.3 v and it depends on its color, varying from a value of approximately 1.7V for a red LED to 3.3V for a blue LED.